Series 20, Episode 10: A Swashbuckling Series Finale

Posted on Nov 17, 2025

Your Task
Series Scores on the Doors
One Episode Ahead Prediction Retrospective
What Have We Learnt Today?

Your Task

We’re at the end of series; the blog post tasks have changed!
Review your one episode ahead prediction for Series 20 of Taskmaster; that is the prediction for episode 10 and the final Series 20 outcome, based on observations up to and include Episode 9. Quantify the probability for the variety of extraordinary events we witnessed.

Figure 1: At last! Correspondence on the last episode of Series 20. Sorry for the delay!

Series Scores on the Doors

Episode 10 Recap and Insights

Episode 10 Performance Report Cards

Episode 10 Performance Grade is based on comparing the current episode performance, to the prior 9 episode(s) performance and where it lies in the distribution.

Figure 2: Episode 10 Performance Report Cards

Figure 3: Contestant Task Performance

Series 20 Task Points Distributions for each Contestant

Past covers tasks up to Episode 9, Current Ep covers tasks in Episode 10.

Figure 3: Contestant Task Performance

And from that swashbuckling finale episode, and as exhibited in Table 2 and 3:

Maisie won the series finale with 17 points.
- This was a very good, above average episode for Maisie, and her 3rd episode win.
Reece and Sanjeev both earned 16 points and were joint 2nd.
- For Reece, this was a good, slightly above average episode for him.
- For Sanjeev, this was a very good episode and appears in this top quartile of episode performance.
Phil had a very bad, below average episode. He accumulated 12 points and finished in 4th place.
Ania rounded out the final episode rankings; she was awarded 10 points in total, and ended up in 5th place for episode.
- This was Ania’s worst episode to date as her prior lowest episode score was 11 in episode 5.
- This is also the first time in the series in which Ania placed 5th in an episode.
Deep diving into Ania’s task performance in this episode, the highest number of task points awarded in this episode was 4.
- Prior to this episode, Ania has the largest number of tasks in which she was awarded 5 points amongst the cast. This title will likely also still hold when considering in all episodes in the series.
- Ania’s poor episode performance can also attributed to her team being disqualified from the team task; they were award 0 points which didn’t help any of that team in their episode score.
This episode featured a task involving a Pythagoras Cup, an ancient (and potentially one of the earliest) practical joke devices from the Roman empire.
- Bernoulli was also mentioned in the same task by Sanjeev, a bit surprising for the statistician inside me as he has his own distribution named after him.

Figure 4: You greedy, greedy man, Mr Shearsmith!

Tangent Time: Science Today, and Science All Your Life

Figure 5: Behold! The Pythagorean Cup!

The Pythagoras Cup

A Pythagoras Cup is a special type of drinking cup that can be used for practical joke purposes, and for teaching unsuspecting victims about the dangers of being greedy. It is also known as a Pythagorean Cup, Greed Cup, Cup of Justice, Anti Greed Goblet, or Tantalus cup, and the cup dates back to the Roman empire.

An original cup has central pillar which deceivingly contains a channel which leads to an opening at the bottom of the cup. When the cup is filled with liquid up to certain point (the height of the central pillar), all liquid (not just the surplus liquid added) will be emptied from the base of the cup through a siphoning effect.¹ The cup holder (and intended victim) will have quite the mess to clear up and explain.

If the liquid does not exceed this limit, the cup functions as normal, and the cup bearer is not penalised for being greedy and their dignity remains in tact. Moderation is rewarded by the lack of humiliation.

Modern day applications of the Pythagoras Cup include toilets² and washing machines (how the fabric softener drawer works).

Figure 6: What kind of witchcraft is this? You’ve ruined my brand new toga! (image 1, image 2)

Bernoulli Principle

But what about this Bernoulli Principle (or Theorem), as alluded to by Sanjeev?

Bernoulli Principle:
A key concept in fluid dynamics that relates speed, presure and height, and the combination of the three maintaining equilibrium.
In particular, assuming constant height, if a fluid’s speed increases, its pressure decreases. And conversely, if the fluid’s speed decreases, its pressure increase.
It’s all about maintaining equilibrium and the conservation of energy. It also has ties to Newton’s 3rd law of motion (every action has equal and opposite reaction).

So in the context of the Pythagoras cup (thanks to the help of this source):

As liquid is poured into the cup (height increases), pressure at the bottom of the cup (the siphoning source) increases.
Once the liquid exceeds the greed limit and the siphoning effect is activated, liquid starts dripping out of the bottom (height decreases) and pressure starts to decrease. The flow rate of the liquid (the speed ) is linear to the pressure (inversely linear for that matter).

It is my belief is that Bernoulli’s principle describes the relationship between rate of flow and pressure in the Pythagoras cup, and not the actual mechanics (as in the siphoning effect), that occurs to make the practical joke work. In fact, Pascal’s Principle of Communicating Vessels is what initiates the siphoning effect.

Figure 7: All is fair and balanced when vessels communicate (figure source)

All is fair and balanced when vessels communicate [(figure source)](https://en.ppt-online.org/235114)

Catfished by Bernoulli

The inner “statistician”³ in me was pleasantly surprised to hear the name Bernoulli mentioned in an episode of Taskmaster. A Bernoulli Distribution (and Random Variable) is used to model phenomena in which there are only two outcomes, with the probability of one outcome only needing to be specified.

The most common example of a Bernoulli Random Variable and Distribution in action is a coin toss (the two outcomes are heads or tails). Other applications include success or failure tests (for example, will Ania be series champion or not), and “on” or “off” events (for example, will Sanjeev be switched “on” and score more than 10 points, or “off” scoring 10 points or less). Note that the probability of the two outcomes occurring do not need to be equal.

Mathematically, we would write this as:

\[ \text{Outcome} = \begin{cases} \text{1: Ania is series champion} & \qquad & \text{with probability } p \\ \text{0: Ania is not series champion} & \qquad & \text{with probability } (1-p) \end{cases} \]

The Bernoulli distribution is one of the key statistical distribution which later forms the basis of the Binomial Distribution (multiple Bernoulli outcomes), which in turn forms the basis of binary classification models (for example logistic regression).

Imagine my surprise however when I learnt that the Bernoulli of this distribution, is not the same Bernoulli of the aforementioned Principle! The Bernoulli Distribution is named after Jacob Bernoulli, whilst the Bernoulli Principle is named after Daniel Bernoulli. I feel catfished!

Are the two Bernoulli’s related at all? Well the Bernoulli family is a renowned Swiss family containing eight academics who collectively made significant impact and contributions in the fields of Mathematics and Physics. Think of the Bernoulli family as the the Mathematical equivalent to the Bach family.

As to how the two Bernoulli are related, the two have an uncle-nephew relationship; Jacob (of Distribution fame) is the elder of the two and heralds from the first generation of Bernoulli academics, whilst Daniel (of Principle fame) is the younger and is from the second generation of academics.

Figure 8: Which Bernoulli we will get, is very much a Bernoulli Random Variable. Jacob Bernoulli (left, senior), Daniel Bernoulli (right, junior)

Which Bernoulli we will get, is very much a Bernoulli Random Variable. [Jacob Bernoulli (left, senior)](https://upload.wikimedia.org/wikipedia/commons/1/19/Jakob_Bernoulli.jpg), [Daniel Bernoulli (right, junior)](https://upload.wikimedia.org/wikipedia/commons/c/cd/Portr%C3%A4t_des_Daniel_Bernoulli_-_edit1.jpg)

The Final Series Scores

Figure 9: The Series 20 race in action!

Well that was a turn out for the books. From Episode 10 and Figure 9:

The final series standings were:
- Joint 1st place for Ania, Maisie and Phil with 151 points.
- Reece placed in 4th place, having accumulated 148 points.
- Sanjeev “Bottom of the Score Board” Bhaskar lived up to his nickname, ending in 5th place with 143 points.
And with this three way series tie, a rather controversial tie breaker occurred. This tie breaker involved recalling (estimating) the number of “T”s in portrait hung in the living room of the Taskmaster house.
- Maisie eventually won this tie breaker and is crowned the Series 20 champion.
A series tie breaker has not happened before in UK Taskmaster history, let alone a series tie breaker between three contestants!
- A series tie breaker has happened in Series 2 of Australian Taskmaster⁴ between Anne Edmonds and Lloyd Langford (who are also partners in real life).
- This series Australian tie breaker seemed a bit fairer and slightly more skill based; it was a live studio tie breaker in which they were tasked to estimate the weight of the Taskmaster trophy.
- Lloyd won the tie breaker and was crowned the Australian champion.

Figure 10: A threesome you say?!

Congratulations Maisie Adams! You’ve successfully managed to escape The Dip and have been crowned the Series 20 Champion!

Figure 11: Never has a gif been so appropriate for how Series 20 panned out eventually…

One Episode Ahead Prediction Retrospective

Recall from Episode 9’s post that our prediction for the cast ranking was: [1st: Ania, 2nd: Phil, 3rd: Maisie, 4th: Reece, 5th: Sanjeev]. This is the one episode ahead prediction for the series ranking for the cast; using data up to including Episode 9, we made a prediction on the series ranking in which a series has 10 episodes.

Evidently this prediction did not occur in the end (it was not observed), and my reputation as an accurate legitimate forecaster is at stake.

Whilst inaccuracy is not a desirable trait, it is somewhat reassurring that the outcome of the series came as a big surprise to the champion herself and by Ed Gamble on the Official Taskmaster podcast (podcast episode link). I think we can appropriately assume that many believed that this outcome had a relatively low chance of occurring.

Which naturally leads to the question of whether we can quantify these chances. In particular, we may be interested in :

Can we quantify the likelihood of the observed series outcome occurring?
- That is, what is the probability of the observed series ranking outcome of [1st: Ania, 1st: Maisie, 1st: Phil, 4th: Reece, 5th: Sanjeev] occurring?
What was the probability of a tie occurring?
- Tie can occur at any rank, and by any number of contestants.
What were the chances of a tie occurring for the championship?
- Tie is between 2 or more contestants.
What were the chances of a 3-way tie for the championship?
What were the chances of the 3-way championship tie being between (Ania, Maisie and Phil), henceforth known as the holy trinity?

This is all based on the known status up to Episode 9.

Figure 12: The disappointment of being inaccurate with my prediction…

Yours Conditionally…

For Questions 3 to 5, it will be worth considering both unconditional and conditional probabilities of these events occurring.

Conditional Distributions are distributions which are conditional on knowing that another event has occurred. This event can include:

knowing that a tie has occurred some where in the series ranking.
knowing that a tie has occurred and that the tie is for the championship (rank 1).

These are different to unconditionally distributions in which we do not know if a tie has occurred or not, and encompasses more uncertainty and unknowns.

Figure 13: Wenches on the Benches Time!

To Tie or Not To Tie (The Knot)? Unconditionally or conditionally…

Figure 14: One Episode Prediction for the Series 20 Outcome

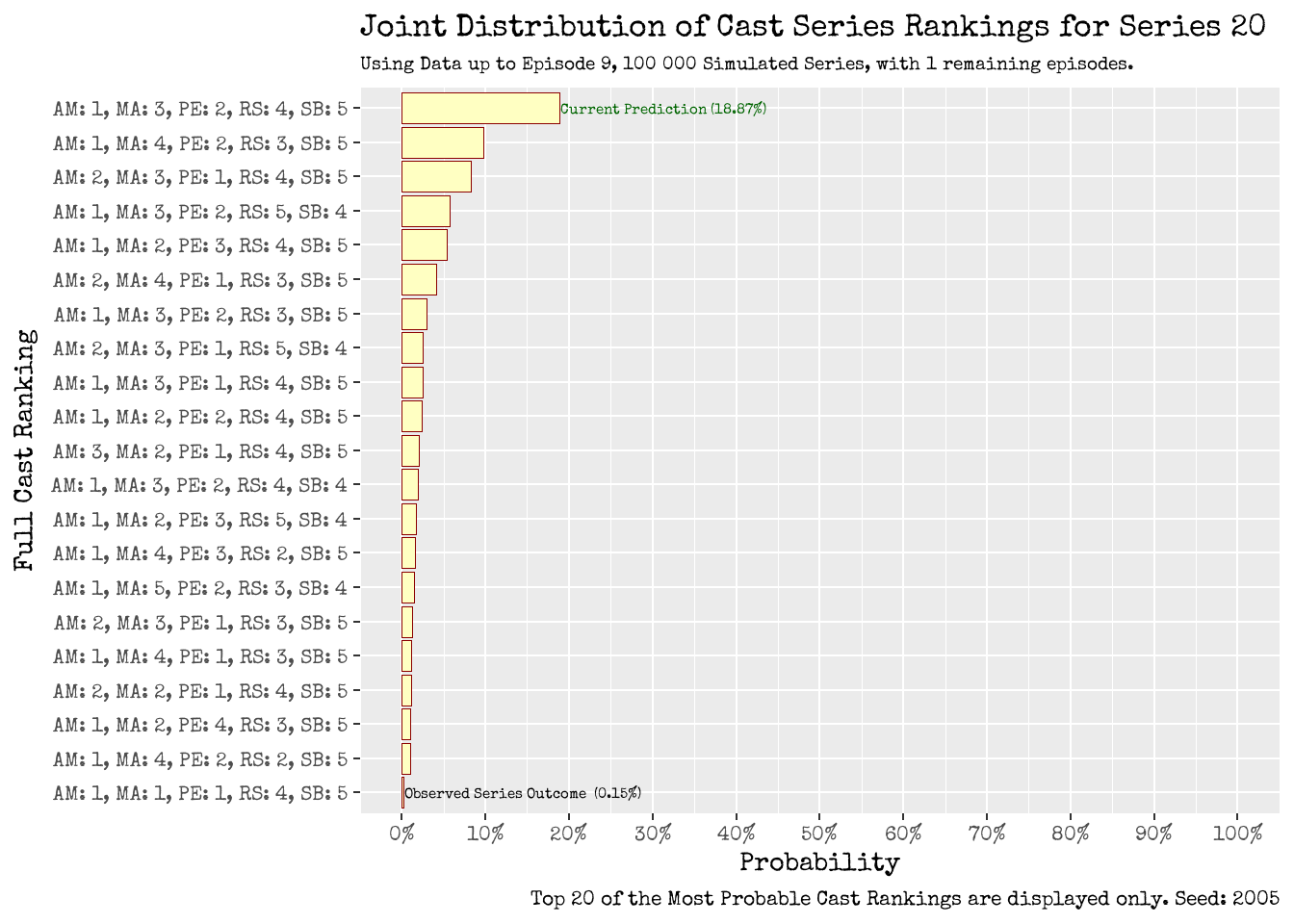
1. Can we quantify the likelihood of the observed series outcome occurring?

That is, what is the probability of the observed series ranking outcome of [1st: Ania, 1st: Maisie, 1st: Phil, 4th: Reece, 5th: Sanjeev] occurring?

From Figure 14, the joint distribution for the series 20 cast rankings based on information up to Episode 9, the observed series outcome of [AM: 1, MA: 1, PE: 1, RS: 4, SB: 5]had a 0.15% chance of occurring. It is ranked as the 62nd most likely series outcome.

To put this into more context, out of the 100,000 timelines we simulated, this observed series outcome occurred in 154.

Figure 15: The cast laughing at how unlikely the observed series outcome was….but it still happened!

Figure 16: Distribution of a Tie Occurring and Not Occurring for Series Rankings

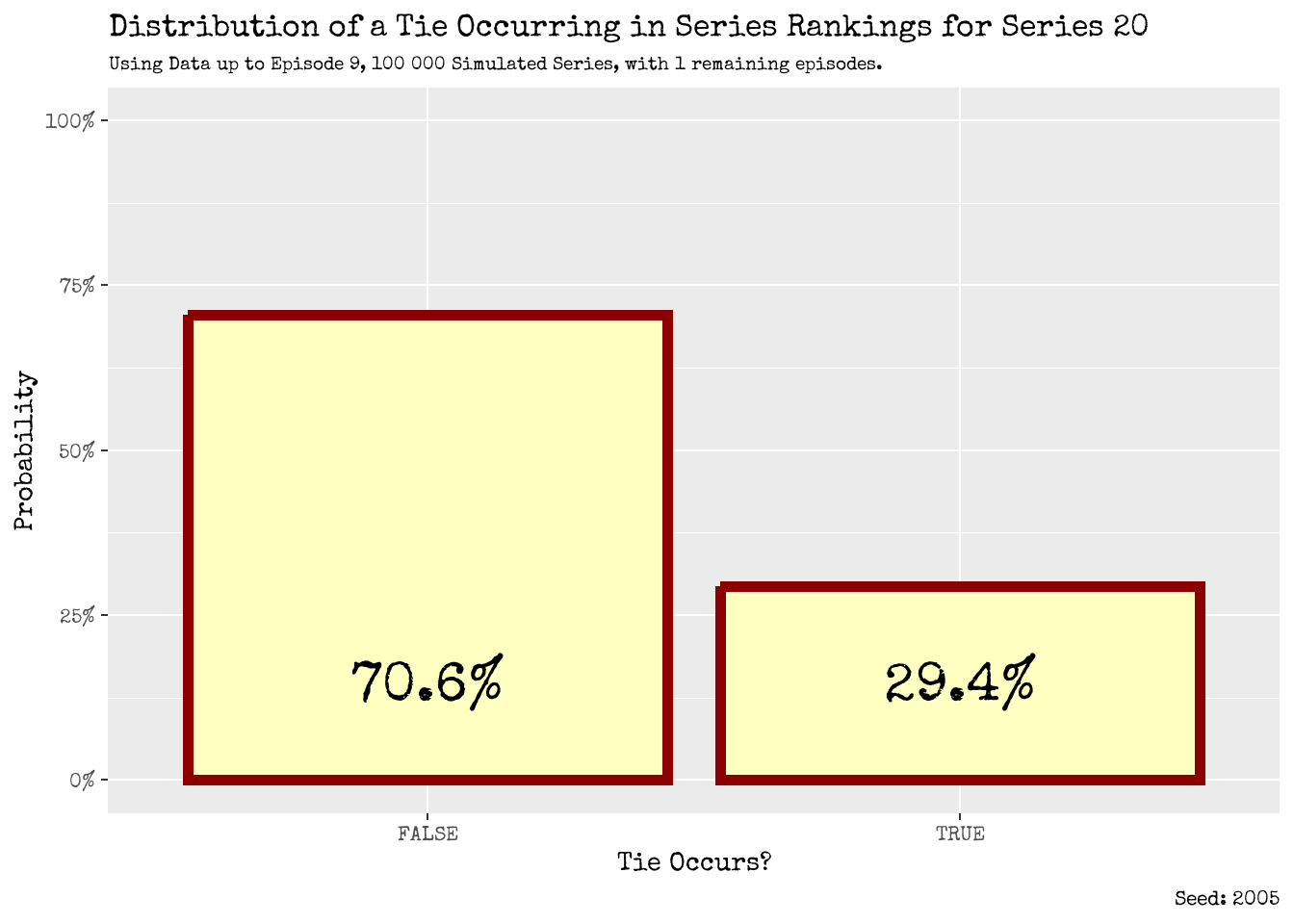
2. What was the probability of a tie occurring?

We estimate that the probability of a tie occurring in any series ranks is 29.4%. This can be seen in Figure 16. As one would expect, the chance of tie occurring is considerably smaller than a tie not occurring.

Figure 17: Conditional Distributions, Conditional on a Tie being present.
(A): Number of Ties in Series Ranking, (B): Ties involving Championship
(C): Max Size of Ties, (D): Championship Tie between Holy Trinity [AM, MA, PE]

Conditional Distributions, Conditional on a Tie being present. <br> (A): Number of Ties in Series Ranking, (B): Ties involving Championship <br> (C): Max Size of Ties, (D): Championship Tie between Holy Trinity `[AM, MA, PE]`

Figure 18: Comparing Unconditional and Uber Conditional, Conditional on a Tie being present.
(A_): Non-Conditional Distributions, (B_): Uber Conditional Distributions, conditioning on a tie occurring and the tie being from the championship.
(_1): Size of Tie, (_2): Tie involving Holy Trinity of [AM, MA, PE]

Comparing Unconditional and Uber Conditional, Conditional on a Tie being present. <br> (A_): Non-Conditional Distributions, (B_): Uber Conditional Distributions, conditioning on a tie occurring **and** the tie being from the championship. <br> (_1): Size of Tie, (_2): Tie involving Holy Trinity of `[AM, MA, PE]`

3. What were the chances of a tie occurring for the championship? Tie is between 2 or more contestants.

Conditional on knowing that a tie occurs some where in the series rankings, the chances that this involves a tie for championship is 26.3%. This can be seen in Figure (17, B).
If we do not know if a tie has or has not occurred in the series ranking, the chances that there is a tie involving the championship is 7.7%. This is the unconditional probability.

Figure 19: Little Alex Horne is finding these probabilities of ties highly amusing!

4. What were the chances of a 3 way tie for the championship?

If we condition on knowing that a tie does occur and that it is for the championship, the probability of it being a 3-way tie is 4.5%.
- This is seen in Figure (18, B1) which assess the maximum size of tie in the cast rankings.
- From Figure (18, B1), we see that there is a inverse exponential relationship between maximum size of tie, and the associated probability. A 2-way tie is the most common with 95.3% probability, whilst a 4-way tie is relatively uncommon with 0.1% chance. This decrease exponential behaviour is expected.
- Yes, 4-way ties for the series championship were possible in our simulations, although a very occurrence! These all Reece joining the tied party. No surprise that Sanjeev was not part of this party, although I don’t think he really minds or cares.
If we condition only on a tie being present (not necessarily for championship), the probability of the largest tie being a 3-way is 3.2%. This is deduced from Figure (17, C).
If we do not condition on anything and are simply considering the probability of a 3-way tie occurring in any position (regardless of whether a tie does or does not occur), the estimated probability of this occurring is 0.9% (see Figure 18, A1).
- This is the most relaxed conditioning and an unconditional probability.

Figure 20: Sanjeev’s response to not being in the simulated 4-way ties…

5. What were the chances of the 3-way championship tie being between (Ania, Maisie and Phil), henceforth known as the holy trinity?

Conditioning that tie does occur and that it is for the championship, the probability that it is a 3-way tie between this holy trinity is 3.0%. See Figure (18, B2).
If we condition on just a tie occurring but not that it is for the championship, the conditional probability of a 3-way between the holy trinity is 0.8% (see Figure (17, D)).
And if we do not condition on any criteria, the unconditional probability of a 3-way tie occurring for the championship involving the holy trinity is 0.2%; see Figure (18, A2).

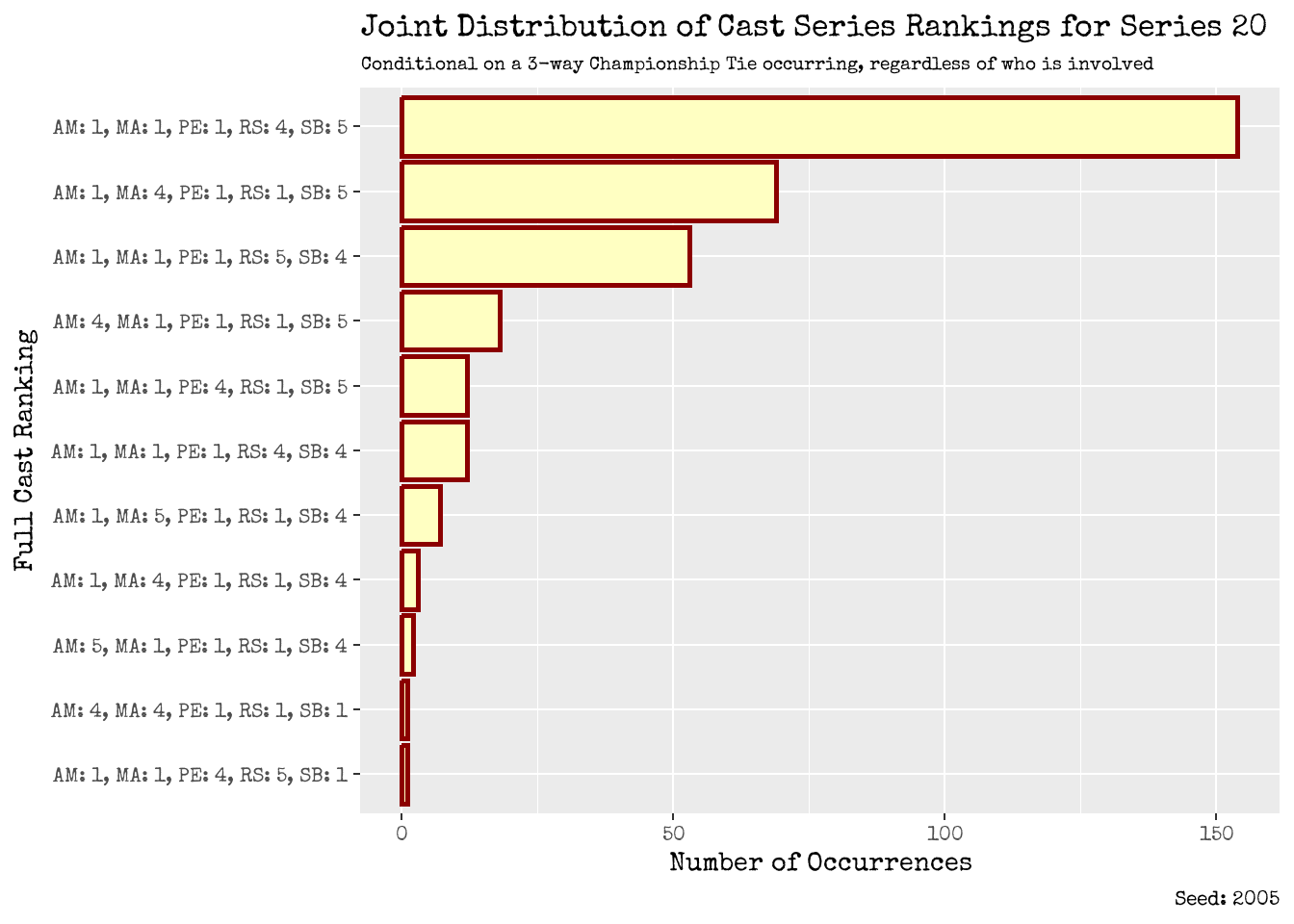
Figure 21: Ménage à trois: Deep Diving into all 3-way Championship Ties

Bonus Remark: Conditional Distribution on Number of Ties in Series Rankings

Figure (17, A) shows the conditional distribution on the number of ties occurring in a cast ranking, conditional on a tie occurring. A tie must include 2 or more contestants placing the same rank.
- The conditional probability of 2 ties occurring is (understandably) considerably less than only 1 tie occurring (5.3% vs 94.7%).
- The probability of 3 or more ties occurring in a cast ranking is 0%. This makes sense given that there are only 5 contestants in the cast, and a tie must feature 2 contestants or more; it’s impossible to have more than 3 ties under these conditions.

Bonus Insight: A deep dive into the ménage à trois championship ties

Figure 21 deep dives in all 3-way championship ties in our simulation of 100,000 timelines. Championship 3-way ties involved all 5 contestants, and not just the holy trinity of interest.
- The aforementioned holy trinity of (Ania, Maisie, Phil) is the most common, occurring about 200 times in our simulated bubble. 150 times featured Reece in 4th place and Sanjeev in 5th, whilst the remaining 50 had Reece in 5th and Sanjeev in 4th.
- The 2nd most common 3-way tie involved an alternative triad of (Ania, Phil, Reece), occurring about 75 times.
- It is also comforting to see that there are some 3-way ties involving Sanjeev, although these occurred with single digit occurrence.
- Another interesting observation is that Phil never slips down to 5th place in these 3-way tie scenarios. He is either part of the championship tie, or placed in 4th place. Even Maisie landed in 5th place in some of simulations.

Figure 22: Ania’s reaction to the fact that she isn’t always in the 3-way championship ties…

Figure 23: We made it through all this talk about unconditional and conditional distributions. It isn’t quite all Greek to me, but it certainly feels like it.

We made it through all this talk about unconditional and conditional distributions. It isn't quite all Greek to me, but it certainly feels like it.

What Have We Learnt Today?

We’ve learnt that:

Series 20 ended in a nail biting finale, with a 3-way tie for championship! The final scoreboard stood at:
- Joint 1st: Ania, Maisie and Phil with 151 points.
- 4th: Reece with 148 points.
- 5th: Sanjeev with 143 points.
The 3-way championship tie (a first in Taskmaster history) was settled by a somewhat controversial tie breaker. Contestants had to “recall (guess) the number of a Ts in a painting at the Taskmaster house”, a painting that they may not have seen for many months since recording at the house.
- Maisie won this controversial tiebreaker and so was crowned champion of series 20.
Based on information up to and including episode 9 of Series 20, we estimate that:
- There was a 0.15% chance of the eventual series ranking outcome occurring, and was the 62nd most probable outcome.
- There was a 29.4% chance of the series ranking outcome featuring a tie.
- There was a 0.2% chance of a championship tie occurring between the holy trinity of (Ania, Maisie, Phil).
  - If we condition ourselves knowing that a tie will occur in the series, this increases to 0.8%.
  - If we further condition ourselves to knowing that there is a tie and it occurs for the championship, this increases further to 3.0%
The existence of one of the earliest practical joke devices in the world (Pythagoras’ Cup) and the experience of being catfished by the Bernoulli legacy.
- These science tangents were also responsible for the delay in getting this post out in a timely fashion. Damn my my curiosity and “thorough” research skills!

Figure 24: Didn’t we have a fun time!

Taskmaster certainly likes to rely on the concept of siphoning quite a bit…↩︎
Does this make it toilet humour then?↩︎
Did I tell you I suffer from imposter syndrome?↩︎
Avid Taskmaster fans will know that it was broadcasted as Series 2, but filmed as Series 3. Who knows why the Australian people decided to do a switch-eroo. I would recommend both of these Series to any UK Taskmaster fans with Jenny Tian and Aaron Chen being welcome additions to my comedy landscape.↩︎